TR-606 / 808 bass drum circuits

Back­ground

The TR-606 and TR-808 were drum ma­chines sold in the early 80s, that used ana­log cir­cuits to pro­duce their in­stru­ment voic­es. Many reim­ple­men­ta­tions of the orig­i­nal cir­cuits ex­ist (both as com­mer­cial and DIY pro­jects, but mostly of the 808), likely due to their iconic sound and the pub­lic avail­abil­ity of cir­cuit schemat­ics from the de­vices’ ser­vice man­u­als.

De­spite this, it is hard to find on­line in­for­ma­tion on how the cir­cuits pro­duce their sound, be­yond the ba­sic prin­ci­ples of op­er­a­tion. ¹

These drum cir­cuits are par­tic­u­larly in­ter­est­ing be­cause the core idea of the cir­cuit is easy to un­der­stand, but there are var­i­ous com­plex­i­ties that af­fect the fi­nal out­put sound (e­spe­cially in the case of the TR-808). This post is an analy­sis of the im­por­tant as­pects of the bass drum cir­cuits from both de­vices.

The gen­eral idea be­hind both cir­cuits is to sim­u­late an drum di­rectly with a cir­cuit that will os­cil­late in re­sponse to be­ing “hit” with a volt­age pulse. ² To do this, one needs to pro­duce a cir­cuit that will have a pair of com­plex con­ju­gate poles, which cor­re­sponds to an im­pulse re­sponse with os­cil­la­tory be­hav­ior.

The Bridged-T Cir­cuit

The core of both ma­chi­nes’ bass drum cir­cuits (and many of the other drum voic­es) is the fol­low­ing bridged-t cir­cuit:

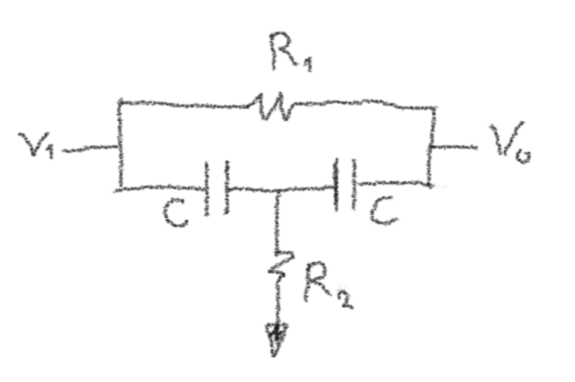
With­out go­ing through the de­riva­tion, the trans­fer func­tion of the cir­cuit is:

$$\frac{ V_o (s) }{ V_1 (s) } = \frac{ s^2 + \frac{ 2 }{ R_1 C } s + \frac{ 1 }{ R_1 R_2 C^2 } } { s^2 + \left( \frac{ 2 }{ R_1 C } + \frac{ 1 }{ R_2 C } \right) s + \frac{ 1 }{ R_1 R_2 C^2 } }$$

On its own, this cir­cuit does not have com­plex poles, since it is a pas­sive RC cir­cuit. How­ev­er, it does have com­plex ze­ros. Given a way to turn ze­ros into poles, the de­sired res­o­nant be­hav­ior can be achieved.

TR-606 Bass Drum

The TR-606 bass drum cir­cuit is the sim­plest ex­ten­sion of the bridged-t cir­cuit:

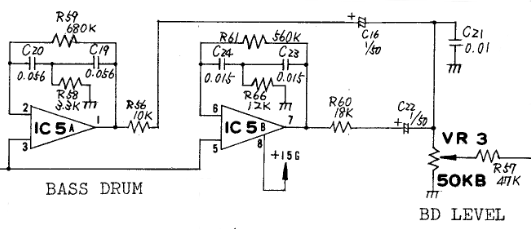
Op amps IC5A and IC5B have the bridged-t con­nected from the out­put to the in­vert­ing in­put (i.e. as neg­a­tive feed­back).

Why does this work ? In gen­er­al, if an am­pli­fier is con­nected with neg­a­tive feed­back, and the gain is large enough (loop gain much larger than 1), then the re­sult­ing trans­fer func­tion is the rec­i­p­ro­cal of the feed­back trans­fer func­tion. This has the ef­fect of ex­chang­ing the poles and ze­ros of the feed­back trans­fer func­tion. In the con­text of the bridged-t, this is how the com­plex ze­ros are turned into the de­sired com­plex poles.

This cir­cuit (bridged-t in the feed­back path of an opamp) is what is pre­sented in the TR-808 ser­vice man­ual as a sim­pli­fied ex­pla­na­tion – ap­ply a pulse and get a drum sound:

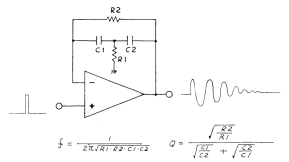
It is of­ten re­ferred to on­line as a band­pass fil­ter (maybe be­cause one would ex­pect a band­pass fil­ter to be used as a res­onator), but this is a mis­lead­ing la­bel.

The trans­fer func­tion from the opam­p’s in­put to its out­put is: ³

$$H_{ 606 }(s) = \frac{ s^2 + \left( \frac{ 2 }{ R_1 C } + \frac{ 1 }{ R_2 C } \right) s + \frac{ 1 }{ R_1 R_2 C^2 } } { s^2 + \frac{ 2 }{ R_1 C } s + \frac{ 1 }{ R_1 R_2 C^2 } }$$

A sec­ond or­der band­pass should only have an $s$ term in the nu­mer­a­tor. In­stead of a band­pass ef­fect, this func­tion will still have unity gain at DC and at high fre­quen­cy. The bode plot for this trans­fer func­tion looks like the fol­low­ing:

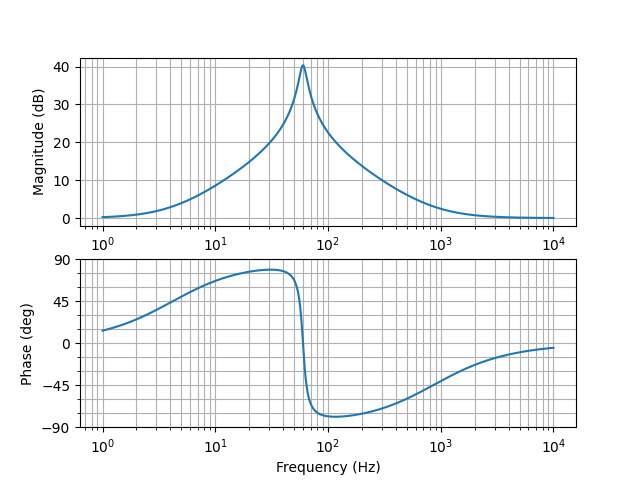
Based on this plot, it is ap­par­ent that while this cir­cuit does have res­o­nance at its nat­ural fre­quen­cy, it does not at­ten­u­ate any other fre­quen­cies (note the y-ax­is, the low­est value is 0 dB – unity gain). As a con­se­quence, the trig­ger pulse is fed through to the out­put. This fea­ture is very im­por­tant to the sound of the cir­cuit, but is­n’t usu­ally men­tioned.

Al­though the feedthrough of the trig­ger pulse seems like a dis­ad­van­tage, it can be help­ful when try­ing to sim­u­late a drum – hear­ing both the hit and the re­sponse to it is pre­sum­ably more re­al­is­tic than mostly hear­ing the re­sponse. ⁴ This was prob­a­bly done on pur­pose, since the TR-808 cir­cuit shows a way to get a true band­pass from this cir­cuit (more on this lat­er), but this was­n’t used in ei­ther cir­cuit for the trig­ger in­put.

TR-606 Trig­ger Cir­cuit

Since the trig­ger pulse is not iso­lated from the au­dio sig­nal, it is worth ex­am­in­ing what it looks like.

The trig­ger cir­cuit ac­tu­ally has two in­puts, one that I’ve an­no­tated as “Ac­cent” (the ex­act name from the man­u­al), and one that I’ve an­no­tated as “En­able” (usu­ally la­beled in the man­ual with the name of the in­stru­ment be­ing trig­gered):

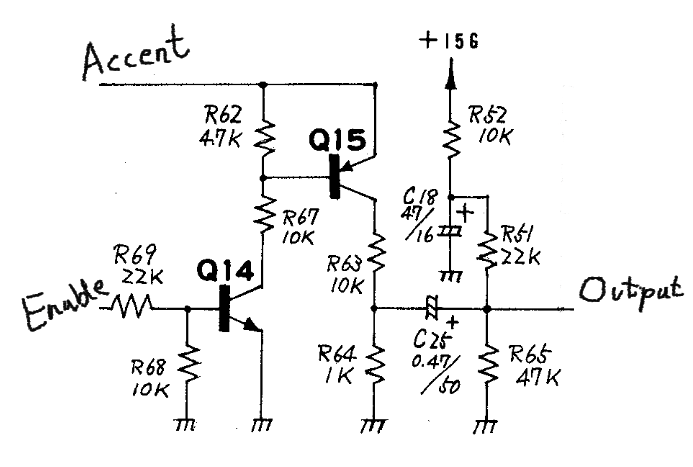
Both in­puts are re­quired to get an out­put, the en­able in­put turns on Q14, which pulls down the base of Q15 to turn it on, but the ac­cent in­put needs some pos­i­tive volt­age for this to hap­pen. Ef­fec­tive­ly, this forms an AND gate.

This cir­cuit has two ad­van­tages that re­late to con­trol­ling many dif­fer­ent sounds at the same time.

1. It’s dif­fi­cult to send a pulse to each in­stru­ment that will play on a beat at the same time (the trig­ger­ing is mi­cro­proces­sor con­trolled). Hav­ing two in­puts solves this prob­lem, each in­stru­ment that will play can be en­abled be­fore the beat, and then the same pulse can be sent to all ac­cent in­puts on the beat, trig­ger­ing only the in­stru­ments that were en­abled.

2. The out­put am­pli­tude is set by the am­pli­tude of the ac­cent in­put (when Q15 is in sat­u­ra­tion, its col­lec­tor will be ~0.3 volts lower than the volt­age on the ac­cent in­put). This al­lows for em­pha­sis of cer­tain beats (by us­ing a larger pulse to make in­stru­ments play­ing on them loud­er), with­out need­ing soft­ware con­trol of out­put vol­ume.

From the pur­pose of analy­sis, as­sume a pulse is pro­duced at the col­lec­tor of Q15. This pulse is re­duced by a fac­tor of 11 by the R63-R64 volt­age di­vider, and ca­pac­i­tively cou­pled to the out­put through C25. The sta­tic out­put level is set by the R52-R51-R65 volt­age di­vider to around 9 volts. This is be­cause the TR-606 does not have a neg­a­tive sup­ply like the TR-808, so the out­put needs to be about mid­way be­tween 0 and 15 volts to al­low the op amp to swing in both di­rec­tions (re­mem­ber that the gain is unity at DC, so the in­put volt­age sets the out­put volt­age).

This is a sim­pli­fied ex­pla­na­tion since C25 (a­long with the re­sis­tors) will pro­duce a high­pass ef­fect. Sim­u­la­tion can be used to find the ac­tual pulse shape: ^{5 6}

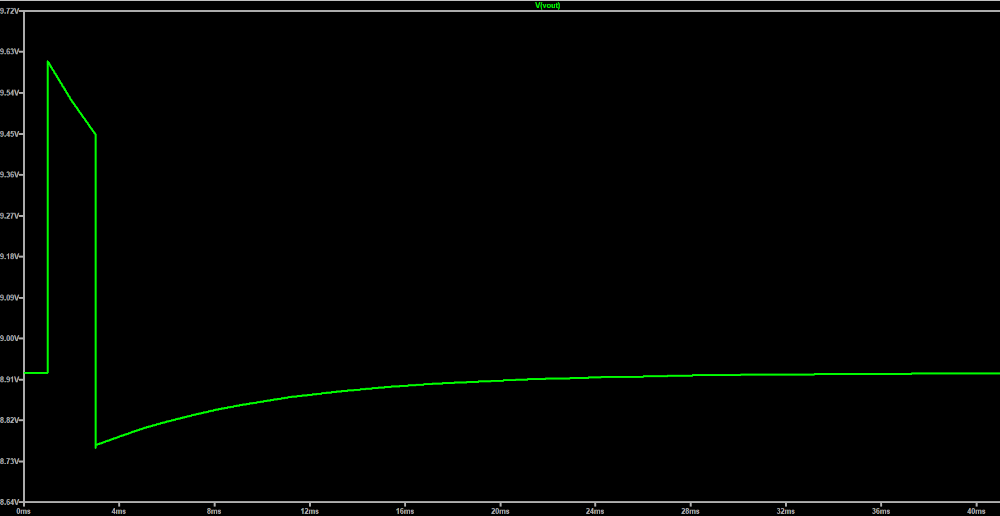
Given this trig­ger pulse, it can be fed to a time do­main sim­u­la­tion of the bass drum trans­fer func­tion, to get an idea of what the out­put would look like:

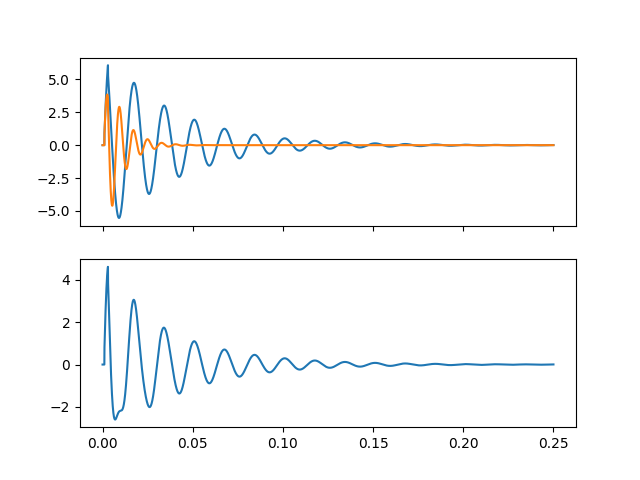
The up­per graph shows the two res­onators sep­a­rate­ly, and the bot­tom graph is a weighted sum sim­i­lar to how the au­dio out­put is made. The higher fre­quency res­onator was de­signed with faster de­cay, so that it mostly af­fects the start of the note. The feedthrough of the trig­ger­ing pulse is also vis­i­ble.

TR-808 Bass Drum

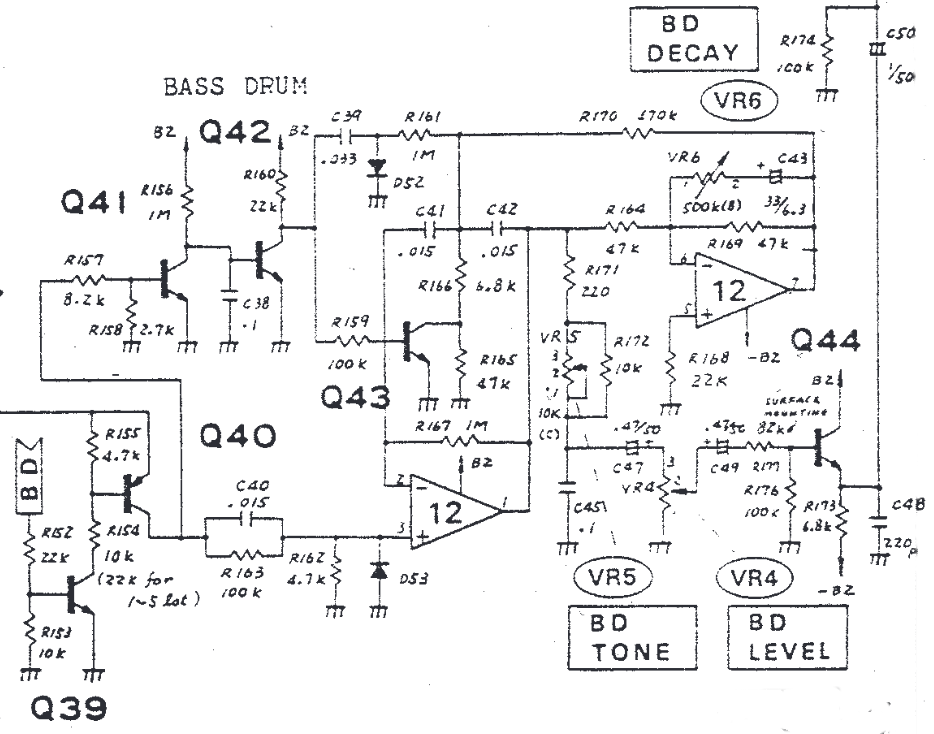
The TR-808 cir­cuit is more com­plex than the one from the TR-606. It uses only one res­onator, but adds sev­eral fea­tures: ⁷

1. Ad­justable de­cay time.
2. Switch­able dou­bling of the res­o­nant fre­quen­cy.
3. Mid-note re­trig­ger­ing.

Ad­justable de­cay time

To un­der­stand how the de­cay time can be ad­just­ed, it makes sense to start from this mod­i­fi­ca­tion of the bridged-t, which in­cludes a sec­ond in­put:

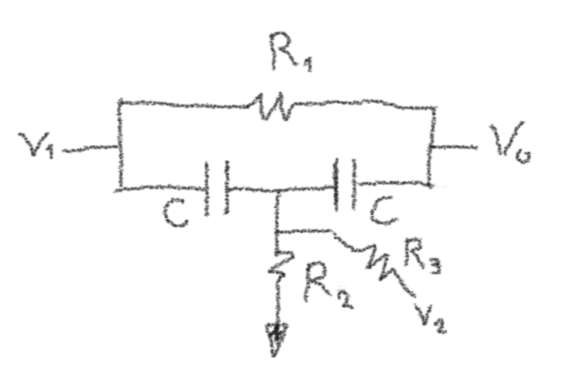
In­tro­duc­ing $R_2^*$ to re­fer to the par­al­lel com­bi­na­tion of $R_2$ and $R_3$ , the trans­fer func­tion from in­put $v_1$ is the same as be­fore, but with $R_2^*$ rather than $R_2$ .

$$\frac{ V_o (s) }{ V_1 (s) } = \frac{ s^2 + \frac{ 2 }{ R_1 C } s + \frac{ 1 }{ R_1 R_2^* C^2 } } { s^2 + \left( \frac{ 2 }{ R_1 C } + \frac{ 1 }{ R_2^* C } \right) s + \frac{ 1 }{ R_1 R_2^* C^2 } }$$

The trans­fer func­tion from the $v_2$ in­put is:

$$\frac{ V_o (s) }{ V_2 (s) } = \frac{ s \frac{ 1 }{ R_3 C } } { s^2 + \left( \frac{ 2 }{ R_1 C } + \frac{ 1 }{ R_2^* C } \right) s + \frac{ 1 }{ R_1 R_2^* C^2 } }$$

Re­mov­ing the parts of the cir­cuit that aren’t im­me­di­ately rel­e­vant to the ad­justable de­cay leaves the fol­low­ing:

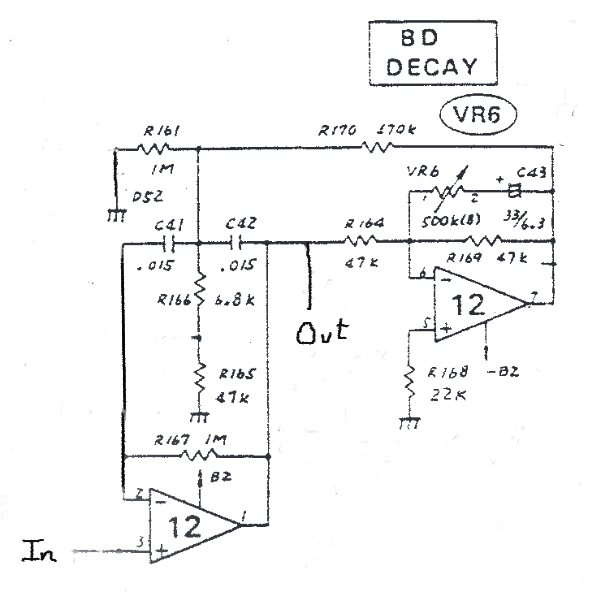
It should be pos­si­ble to rec­og­nize the bridged-t cir­cuit. R166 and R165 form $R_2$ and R170 is $R_3$ . R161 can be added in par­al­lel with $R_2$ or just ig­nored since it is some­what large (the ex­act com­po­nent val­ues don’t mat­ter to un­der­stand­ing how the cir­cuit works, and treat­ing it as grounded is an ap­prox­i­ma­tion any­way).

Like in the 606 cir­cuit, the $v_1$ in­put of the bridged-t is con­nected to the out­put of the opamp. Ad­di­tion­al­ly, the sec­ond op amp forms an in­vert­ing am­pli­fier con­nected be­tween the out­put and the $v_2$ in­put of the bridged-t. As a sig­nal flow graph, this looks like the fol­low­ing (where K is the gain of the in­vert­ing am­pli­fier):

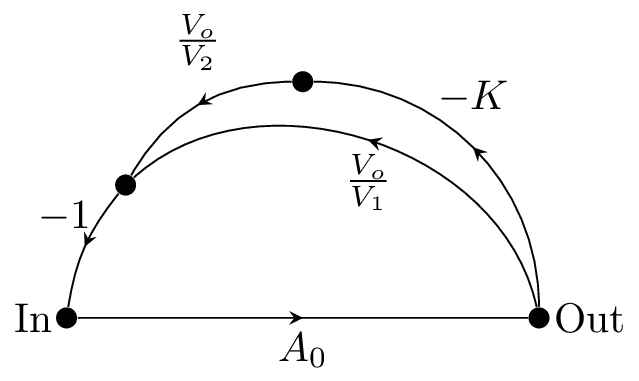
The same logic ap­plies as be­fore: since the op amp gain is large, the re­sult­ing trans­fer func­tion is the rec­i­p­ro­cal of the feed­back trans­fer func­tion. The feed­back trans­fer func­tion is the sum of both par­al­lel feed­back paths: ⁸

$$H_{ 808^1 }(s) = \frac{ 1 }{ \frac{ V_o (s) }{ V_1 (s) } - K \frac{ V_o (s) }{ V_2 (s) } } = \frac{ s^2 + \left( \frac{ 2 }{ R_1 C } + \frac{ 1 }{ R_2^* C } \right) s + \frac{ 1 }{ R_1 R_2^* C^2 } } { s^2 + \left( \frac{ 2 }{ R_1 C } - K \frac{ 1 }{ R_3 C } \right) s + \frac{ 1 }{ R_1 R_2^* C^2 } }$$

The gain of the feed­back op amp changes the co­ef­fi­cient of s in the de­nom­i­na­tor, which af­fects how close the poles are to the imag­i­nary ax­is, and there­fore how fast the os­cil­la­tions de­cay. If the co­ef­fi­cient gets to 0, the sys­tem will be un­sta­ble, so with $R_1 = 1 \tex­t{M}\Omega$ and $R_3 = 470 \tex­t{k}\Omega$ , this puts the up­per limit for K at just un­der 1. This cor­re­sponds closely to the range of ad­just­ment of the de­cay po­ten­tiome­ter, VR6, which al­lows ad­just­ment of the (AC) gain of the feed­back opamp.

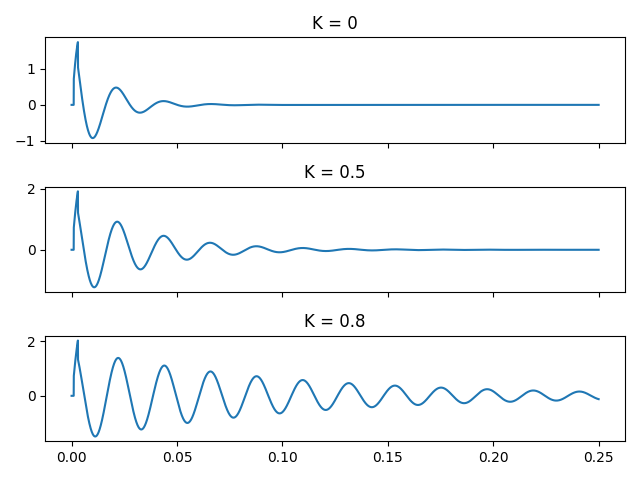
The de­cay ad­just­ment ef­fect can be con­firmed with time-­do­main sim­u­la­tion of the trans­fer func­tion at var­i­ous val­ues of K:

Switch­able dou­bling of the res­o­nant fre­quency

Here’s what the ser­vice man­ual has to say about this:

Im­me­di­ately af­ter a trig­ger pulse is fed into the gen­er­a­tor, the fil­ter’s time con­stant – when AC­CENT is present – is halved and has a res­o­nance on twice its in­her­ent fre­quency for a half cy­cle pe­ri­od, then on the fixed fre­quency with de­cay­ing am­pli­tude. This chang­ing fre­quency will sound a punchier crisp bass.

The mech­a­nism is fairly easy to un­der­stand, Q43 is placed to ef­fec­tively short out R165 when turned on. While R165 is short­ed, the $R_2$ re­sis­tance is only R166, so the res­o­nant fre­quency is in­creased.

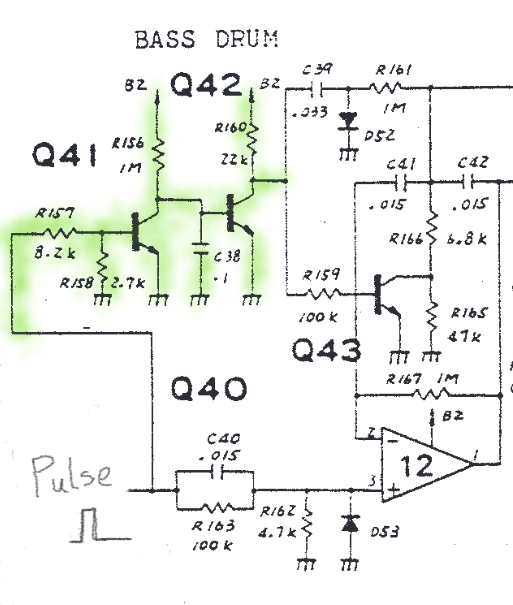
Q41 and Q42 act to ex­tend the pulse du­ra­tion to con­trol how the long Q43 is en­abled for. The trig­ger pulse en­ables Q41, which pulls down the base of Q42, turn­ing it off. When Q42 is off, the base of Q43 is pulled up by R160, turn­ing it on. Af­ter the trig­ger pulse ends, C38 needs to charge through R156 in or­der for Q42 to be turned back on. This charg­ing time con­trols how long the fre­quency dou­bling is en­abled for.

There is an­other ef­fect re­lated to this cir­cuit: a bass drum note from the TR-808 ap­par­ently drifts slightly lower in fre­quency as it de­cays. When the volt­age at the col­lec­tor of Q43 is neg­a­tive, the base-­col­lec­tor junc­tion is for­ward bi­ased and the tran­sis­tor will con­duct slightly in the re­verse di­rec­tion. ⁹ Be­cause of this, there is some leak­age cur­rent dur­ing part of the out­put cy­cle, which can be thought of as a slightly lower $R_2$ re­sis­tance. This cur­rent de­pends on the am­pli­tude at the col­lec­tor of Q43, so as the note de­cays the ef­fect is less­ened, and the fre­quency ap­proaches the the­o­ret­i­cal value from the trans­fer func­tion. ¹⁰

Mid-note re­trig­ger­ing

Also from the ser­vice man­u­al:

When Q42 turns on af­ter 4ms, cur­rent dis­charg­ing from C39 via R161 pro­duces a re­trig­ger­ing pulse. At this time the gen­er­a­tor os­cil­lates on the in­her­ent fre­quen­cy.

The in­ter­est­ing part is that this re­trig­ger­ing pulse is not on the same in­put as the ini­tial pulse. In­stead, it is ap­plied via R161 to the cen­tral node of the bridged-t. As­sum­ing for sim­pli­fi­ca­tion that the other side of R161 (with C39) can be mod­eled as a volt­age source, the re­trig­ger­ing pulse is in­put in much the same way as the feed­back: via a re­sis­tor in par­al­lel with $R_2$ .

In terms of the sig­nal flow graph, with $v_3$ be­ing the re­trig­ger in­put, this looks like the fol­low­ing:

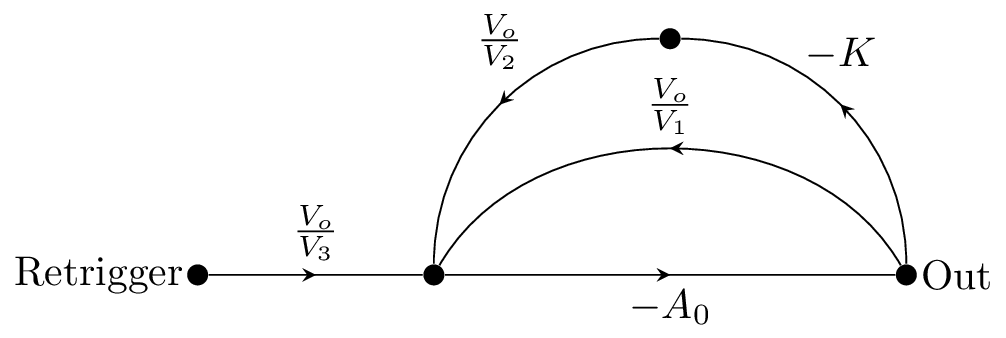
This is the pre­vi­ous trans­fer func­tion in se­ries with the one from $v_3$ to the in­vert­ing in­put. ¹¹ Let­ting $R_4$ be the in­put re­sis­tor for the re­trig­ger in­put (R161), the full trans­fer func­tion is:

$$H_{ 808^2 }(s) = \frac{ V_o (s) }{ V_3 (s) } \frac{ -1 }{ \frac{ V_o (s) }{ V_1 (s) } - K \frac{ V_o (s) }{ V_2 (s) } } = \frac{ -s \frac{ 1 }{ R_4 C } } { s^2 + \left( \frac{ 2 }{ R_1 C } - K \frac{ 1 }{ R_3 C } \right) s + \frac{ 1 }{ R_1 R_2^* C^2 } }$$

This trans­fer func­tion ac­tu­ally de­scribes a band­pass fil­ter, ¹² un­like the one from the nor­mal trig­ger in­put. This makes sense since hav­ing the a pulse feed through in the mid­dle of the note is much more of a prob­lem than at the start – there’s no way that it would seem re­al­is­tic. As men­tioned pre­vi­ous­ly, this also shows that the pulse feedthrough of the ini­tial trig­ger was likely a de­sired ef­fect, since this topol­ogy could have been used to avoid it.

Con­clu­sion

Many in­ter­est­ing as­pects of these cir­cuits that are not com­monly men­tioned are rel­a­tively straight­for­ward to an­a­lyze from an ana­log cir­cuit/­con­trol the­ory per­spec­tive. My sug­gested key take­aways for build­ing TR-606/TR-808 in­spired de­signs are:

• The bridged-t core of both cir­cuits is not a band­pass as is some­times claimed. At­ten­tion should be paid to the pulse that is dri­ving the cir­cuit, it will be heard in the out­put.

• It’s easy to add ex­tra in­puts in par­al­lel with the grounded re­sis­tor in the bridged-t for fea­tures like the de­cay ad­just­ment feed­back loop or re­trig­ger­ing.

• A side ef­fect of in­clud­ing the tran­sis­tor for switch­able fre­quency dou­bling is a sub­tle pitch drift as the note de­cays. It takes rel­a­tively lit­tle leak­age cur­rent to cause this ef­fect.